I de mikrokosmos jag är inbäddad i är trie-datastrukturer inte så populära. Denna miljö består främst av datavetare och, i ett mindre antal, mjukvaruingenjörer som arbetar med Natural Language Processing (NLP).
För en kort tid sedan hamnade jag i en intressant diskussion om när man ska använda trie eller hash table. Även om det inte fanns något nytt i den diskussionen som jag kan rapportera här, som för- och nackdelar med var och en av dessa två datastrukturer (om du googlar lite hittar du många länkar som tar upp dem), så var det som var nytt för mig en speciell typ av trie som kallas Patricia Trie och att i vissa scenarier presterar denna datastruktur jämförbart både i bearbetningstid och utrymme med hashtabellen, samtidigt som den tar upp uppgifter som att lista strängar med gemensamt prefix utan extra kostnad.
Med detta i åtanke sökte jag efter en berättelse eller blogg som skulle hjälpa mig att på ett enkelt sätt (eufemism för lathet) förstå hur PATRICIA-algoritmen fungerar, och som särskilt skulle fungera som en genväg till att läsa den 21 sidor långa artikel som publicerades 1968. Tyvärr lyckades jag inte med denna sökning, vilket gjorde att jag inte hade något alternativ till att läsa det.
Mitt mål med denna berättelse är att fylla ovanstående lucka, dvs. att ha en berättelse som i lekmannatermer beskriver den aktuella algoritmen.
För att uppnå mitt mål kommer jag först, och kortfattat, att introducera, för dem som inte är bekanta med försök, denna datastruktur. Efter denna introduktion kommer jag att lista de mest populära tries som finns, vilket gör det möjligt för mig att implementera och i detalj beskriva hur PATRICIA Trie fungerar och varför de presterar så bra. Jag kommer att avsluta den här berättelsen med att jämföra resultaten (prestanda och utrymmesförbrukning) i två olika tillämpningar: den första är en ordräkning (<WORD, FREQUENCY> tuples) baserad på en ganska stor text, och den andra är att bygga en <URL, IP> tuples, baserad på en lista med mer än 2 miljoner URL:er, som består av kärnan i en DNS-server. Båda programmen byggdes på Hash Map och Patricia Trie.
Enligt definitionen av Sedgewick och Wayne från Princeton University i deras bok Algorithms – Fourth Edition (förlag: Addison-Wesley) är en trie, eller prefixträd, ”en datastruktur som byggs upp av tecknen i söknyckeln för att vägleda sökningen”. Denna ”datastruktur består av noder som innehåller länkar som antingen är noll eller hänvisar till andra noder. Varje nod pekas ut av endast en annan nod, som kallas dess förälder (med undantag för en nod, roten, som inte har några noder som pekar ut den), och varje nod har S länkar, där S är alfabetets storlek (eller charset)”.
Figur 1 nedan, som följer ovanstående definition, innehåller ett exempel på en trie.

Rotnoden har ingen etikett. Den har tre barn: noder med nyckel ”a”, ”h” och ”s”. I det nedre högra hörnet av figuren finns en tabell som listar alla nycklar med deras respektive värde. Från roten kan vi gå till ”a” -> ”i” -> ”r”. Denna sekvens bildar ordet ”air” med ett värde (t.ex. det antal gånger ordet förekommer i en text) på 4 (värdena finns i en grön ruta). Enligt konvention har ett befintligt ord i en symboltabell ett värde som inte är noll. Även om ordet ”airway” finns på engelska finns det alltså inte med i denna trie, eftersom värdet för noden med nyckeln ”y” enligt konventionen är noll.
Värdet ”air” är också ett prefix för orden: ”air” är också ett prefix för orden ”airplane” och ”airways”. Sekvensen ’h’ -> ’a’ bildar prefixet för ”har” och ”hatt” liksom sekvensen ’h’ -> ’o’ bildar prefixet för ”hus” och ”häst”.
Förutom att fungera väl som datastruktur för, låt oss säga, ett lexikon, tjänar den också som en viktig del av ett kompletteringsprogram. Ett system skulle kunna föreslå orden ”airplane” och ”airways” efter att en användare har skrivit ordet ”air”, genom att gå igenom delträdet vars rot är noden med nyckeln ”r”. En ytterligare fördel med denna struktur är att man kan få en ordnad lista över de befintliga nycklarna, utan extra kostnad, genom att gå igenom tresteget i en ordnad riktning, genom att stapla en nods barn på varandra och gå igenom dem från vänster till höger.
I figur 2 exemplifieras nodens anatomi.

Den intressanta biten i denna anatomi är att barnpekare vanligtvis lagras i en array. Om vi representerar en teckenuppsättning S, till exempel Extended ASCII, behöver vi en array med en storlek på 256 tecken. När vi har ett barns tecken kan vi få tillgång till dess pekare i dess förälder på O(1)-tid. Med tanke på att ordförrådets storlek är N och att storleken på det längsta ordet är M, är trie-djupet också M och det tar O(MN) att genomkorsa strukturen. Om vi betänker att N normalt sett är mycket större än M (antalet ord i en korpus är mycket större än storleken på det längsta ordet) kan vi betrakta O(MN) som linjär. I praktiken är denna matris gles, dvs. majoriteten av noderna har mycket färre barn än S. Dessutom är den genomsnittliga storleken på orden också mindre än M, vilket innebär att det i praktiken i genomsnitt tar O(logₛ N) att söka efter en nyckel och O(N logₛ N) att genomkorsa hela strukturen.
Det finns två huvudproblem med denna datastruktur. Det ena är utrymmeskonsumtion. På varje nivå L, med början vid noll, finns det, assimptotiskt sett, Sᴸ pekare. Om detta med Extended ASCII, dvs. 256 tecken, är ett problem i begränsade minnesenheter, förvärras situationen om man beaktar alla Unicode-tecken (65 000 av dem). Det andra problemet är antalet noder med bara ett barn, vilket försämrar inmatnings- och sökprestanda. I exemplet i figur 1 är det bara roten, nyckeln ”h” på nivå 1, nycklarna ”a” och ”o” på nivå 2 och nyckeln ”r” på nivå 3 som har mer än ett barn. Med andra ord har endast 5 noder av 27 två eller fler barn. Alternativen till denna struktur tar främst upp dessa problem.
För att beskriva alternativet (PATRICIA Trie) kommer jag att besvara följande fråga: Varför alternativ om vi kan använda en hashtabell i stället för en array? Hashtabellen hjälper verkligen till att spara minne med liten prestandaförlust, men löser inte problemet. Ju högre man befinner sig i trie (närmare nivå noll) desto större är sannolikheten att nästan alla tecken i alla teckenuppsättningar måste behandlas. Väl implementerade hashtabeller, som den i Java (definitivt bland de bästa, kanske den bästa), börjar med en standardstorlek och ändrar automatiskt storlek enligt ett tröskelvärde. I Java är standardstorleken 16 med ett tröskelvärde på 0,75 och den fördubblar sin storlek i var och en av dessa operationer. Med tanke på Extended ASCII kommer hashtabellen att ändras till 512 när antalet barn i en nod når 192, trots att den bara behöver 256 i slutet.
Radix Trie
Eftersom PATRICIA Trie är ett specialfall av Radix Trie, kommer jag att börja med den senare. I Wikipedia definieras en Radix Trie som ”en datastruktur som representerar en utrymmesoptimerad trie… där varje nod som är det enda barnet slås samman med sin förälder… Till skillnad från vanliga träd (där hela nycklar jämförs i massor från början fram till ojämlikhetspunkten) jämförs nyckeln i varje nod bit för bit, där kvantiteten av bitar i den biten i den noden är radix r i Radix Trie”. Denna definition kommer att bli mer begriplig när vi exemplifierar denna triangel i figur 3.
Antalet barn r för en nod i en radix trie bestäms av följande formel där x är antalet bitar som krävs för att jämföra den ovan nämnda chunk-of-bits:
Ovanstående formel fastställer att antalet barn i en Radix Trie alltid är en multipel av 2. Till exempel för en 4-Radix Trie är x = 2. Detta innebär att vi måste jämföra delar av två bitar, ett par bitar, eftersom vi med dessa två bitar representerar alla decimaltal från 0 till 3, totalt 4 olika tal, ett för varje barn.
För att bättre förstå ovanstående definitioner, låt oss betrakta exemplet i figur 3. I detta exempel har vi en hypotetisk teckenuppsättning som består av 5 tecken (NULL, A, B, C och D). Jag valde att representera dem med hjälp av endast 4 bitar (tänk på att detta inte har något att göra med r, man behöver bara 3 bitar för att representera 5 tecken, utan har att göra med att det är lätt att rita exemplet). I det övre vänstra hörnet av figuren finns en tabell som visar varje tecken till dess bitrepresentation.
För att infoga tecknet ”A” kommer jag att jämföra det bitvis med NULL-tecknet. I det övre högra hörnet av figur 3, inom rutan märkt med 1 i en gul diamant, kan vi se att dessa två tecken skiljer sig åt i det första paret. Detta första par representeras med rött i A:s 4-bitarsrepresentation. DIFF innehåller alltså bitpositionen där det olika paret slutar.
För att infoga tecken ”B” måste vi jämföra det bitvis med tecken ”A”. Denna jämförelse finns i diamantrutan märkt med 2. Skillnaden faller den här gången på det andra bitparet, i rött, som slutar på position 4. Eftersom det andra paret är 01 skapar vi en nod med nyckel B och pekar adressen 01 i nod A till den. Denna länk kan ses i den nedre delen av figur 3. Samma procedur gäller för att infoga tecknen ”C” och ”D”.

I exemplet ovan ser vi att det första paret (01 i blått) är prefix för alla tecken som infogas.
Detta exempel tjänar till att beskriva chunk-of-bits-jämförelse, utrymmesoptimering (endast fyra barn i det här fallet, oavsett teckenuppsättningens storlek) och föräldra/barn-sammanslagning (lagras i barnnoderna endast de bitar som skiljer sig från roten) som nämns i Radix Trie-definitionen ovan. Trots detta finns det fortfarande en länk som pekar på en nollnod. Sparsamhet är direkt proportionell mot r och tries djup.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, oktober 1968) . Ja, PATRICIA är en akronym!
PATRICIA Trie definieras här av tre regler:
- Varje nod (TWIN är PATRICIAs ursprungliga term) har två barn (r = 2 och x = 1 i Radix Trie-termer);
- En nod delas endast upp i ett prefix (L-PHRASE i PATRICIAs termer) med två barn (varje barn bildar en BRANCH som är PATRICIAs ursprungliga term) om två ord (PROPER OCCURRENCE i PATRICIAs termer) har samma prefix; och
- Varje ordändelse kommer att representeras med ett annat värde i noden än noll (END-markering i PATRICIAs ursprungliga nomenklatur)
Regel nummer 2 ovan innebär att längden på prefixet på varje nivå är större än längden på prefixet från den föregående nivån. Detta kommer att vara mycket viktigt i de algoritmer som stöder PATRICIA-operationer som att infoga ett element eller hitta ett annat.
Med utgångspunkt i ovanstående regler kan man definiera noden på följande sätt. Varje nod har en förälder, förutom roten, och två barn, ett värde (vilken typ som helst) och en variabel diff som anger positionen där splittringen är i nyckelbitkoden

För att använda PATRICIA-algoritmen behöver vi en funktion som, givet två strängar, returnerar positionen för den första biten, från vänster till höger, där de skiljer sig åt. Vi har redan sett att detta fungerar för Radix Trie.
För att använda Trie med hjälp av PATRICIA, dvs. för att infoga eller hitta nycklar i den, behöver vi två pekare. Den ena är parent, som initieras genom att den pekas på rotnoden. Den andra är child, som initieras genom att peka på rotens vänstra barn.
Om vad som följer kommer variabeln diff att hålla den position där nyckeln som sätts in skiljer sig från child.key. Enligt regel nummer 2 definierar vi följande två ojämförelser:
Let found pekar på den nod där sökningen efter en nyckel slutar. Om found.key skiljer sig från den sträng som infogas kommer diff att beräknas, via en ComputeDiff-funktion, med hjälp av denna sträng och found.key. Om de är lika finns nyckeln i strukturen och, som i alla symboltabeller, ska värdet returneras. En hjälpmetod kallad BitAtPosition, som hämtar biten på en specifik position (0 eller 1), kommer att användas under operationerna.
För att söka måste vi definiera en Search(key)-funktion. Dess pseudokod finns i figur 4.

Den andra funktionen som vi kommer att använda i den här historien är Insert(key). Dess pseudokod finns i figur 6.

I ovanstående pseudokod finns det en metod för att skapa en nod som heter CreateNode. Dess argument kan förstås från figur 4.
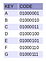
För att exemplifiera hur en PATRICIA Trie fungerar föredrar jag att vägleda läsaren i en steg-för-steg-operation för att slutföra införandet av 7 tecken (”A”, ”B”, ”C”, ”D”, ”E”, ”F” och ”G” som specificeras i figur 7 bredvid) i deras naturliga ordning. I slutet har man förhoppningsvis förstått hur denna datastruktur fungerar.
Tecknet A är det första som ska införas. Dess bitkod är 01000001. Precis som med Radix Trie kommer vi att jämföra denna bitkod med den i roten som för tillfället är noll, så vi jämför 00000000 med 01000001. Skillnaden faller på position 2 (här eftersom x = 1 jämför vi bit för bit istället för ett par av dem).

För att skapa noden måste vi peka på det vänstra och det högra barnet till deras respektive efterföljare. Eftersom den här noden är roten pekar dess vänstra barn per definition på sig själv medan dess högra barn pekar på null. Detta kommer att vara den enda nollpekaren i hela triangeln. Kom ihåg att roten är den enda noden som inte har någon förälder. Värdet, som i vårt exempel kommer att vara heltal för att efterlikna ett program för ordräkning, sätts till 1. Resultatet av denna infogning visas i figur 8.
Nästan kommer vi att infoga tecken B med bitkod 01000010. Det första vi gör är att kontrollera om detta tecken redan finns i strukturen. För att göra detta kommer vi att söka efter det. Det är enkelt att söka i en PATRICIA Trie (se pseudokod i figur 5). Efter att ha jämfört rotens nyckel med B drar man slutsatsen att de är olika, så vi fortsätter genom att skapa två pekare: förälder och barn. Till att börja med pekar parent på roten och child på rotens vänstra barn. I det här fallet pekar båda på nod A. Enligt regel nummer 2 kommer vi att iterera strukturen medan ojämförelsen (1) är sann.
I detta ögonblick är parent.DIFF lika med, och inte mindre än, child.DIFF. Detta bryter oekvationen (1). Eftersom child.VALUE är annorlunda än null (lika med 1) jämför vi tecknen. Eftersom A är annorlunda än B betyder det att B inte finns med i triangeln och måste infogas.
För att infoga börjar vi återigen med att definiera förälder och barn som tidigare, dvs. förälder pekar på roten och barn pekar på dess vänstra nod. Iterationen genom strukturen måste följa olikheterna (1) och (2). Vi fortsätter med att beräkna diff, som är skillnaden, bitvis, mellan B och child.KEY, som i detta skede är lika med A (skillnaden mellan bitkoderna 01000001 och 01000010) . Skillnaden faller på bit på position 7 , så diff = 7.

I detta ögonblick pekar förälder och barn på samma nod (på nod A, roten). Eftersom olikhet (1) redan är falsk och child.DIFF är mindre än diff, kommer vi att skapa nod B och peka parent.LEFT på den. På samma sätt som vi gjorde med nod A måste vi peka nodens barn B någonstans. Biten på position 7 i B är 1, så nodens högra barn B kommer att peka på sig själv. Nodens vänstra barn B kommer att peka på parent, roten i det här fallet. Slutresultatet visas i figur 9.
Där vi pekar nodens B-barn till vänster på sin förälder möjliggör vi den uppdelning som nämns i regel nummer 2. När vi infogar ett tecken vars diff ligger mellan 2 och 7 kommer denna pekare att skicka oss tillbaka till rätt position från vilken man infogar det nya tecknet. Detta kommer att ske när vi sätter in tecken D.
Men innan dess måste vi sätta in tecken C med en bitkod som är lika med 01000011. Pointer parent kommer att peka på nod A (roten). Den här gången, till skillnad från när vi sökte efter tecken B, pekar barnet på nod B (då pekade båda pekarna på roten).
I det här ögonblicket gäller oekvation (1) (parent.DIFF är mindre än child.DIFF), så vi uppdaterar båda pekarna genom att ställa in parent till child och child till nod B:s högra barn, eftersom C:s bit i position 7 är 1.
Efter uppdateringen pekar båda pekarna på nod B, vilket bryter oekvation (1). Liksom tidigare jämför vi child.KEY bitkod med C:s bitkod (01000010 med 01000011) och konstaterar att de skiljer sig åt i position 8. Eftersom C:s bit i position 7 är 1 kommer den nya noden (nod C) att vara höger barn till B. I position 8 är C:s bit 1, vilket gör att vi sätter nod C:s högra barn till sig själv, medan dess vänstra barn pekar på föräldern, nod B i detta ögonblick. Den resulterande trie är i figur 10.

Nästa tecken är D (bitkod 01000100). Precis som vi gjorde när vi infogade tecken C kommer vi inledningsvis att ställa in pekaren parent till nod A och pekaren child till nod B. Inekvation (1) är giltig, så vi uppdaterar pekarna. Nu pekar förälder på nod B och barn pekar på nod B:s vänstra barn, eftersom D:s bit vid position 7 är 0. Till skillnad från att infoga tecken C pekar nu barn tillbaka till nod A, vilket bryter oekvationen (1). Återigen beräknar vi skillnaden mellan A och D bitkoder. Nu är skillnaden 6. Återigen ställer vi in förälder och barn som vi brukar göra. Medan oekvation (1) är giltig, är oekvation (2) det inte. Detta innebär att vi kommer att infoga D som det vänstra barnet till A. Men hur är det med D:s barn? På position 6 är D:s bit 1 så dess högra barn pekar på sig själv. Det intressanta är att nodens D:s vänstra barn nu kommer att peka på nod B, vilket leder till den trie som visas i figur 11.

Nästan är tecknet E med bitkoden 01000101. Sökfunktionen returnerar noden D. Skillnaden mellan tecknen D och E faller på biten i position 8. Eftersom E:s bit i position 6 är 1 kommer den att placeras till höger om D. Trie-strukturen illustreras i figur 12.

Det intressanta med att infoga tecken F är att dess plats är mellan tecknen D och E, eftersom skillnaden mellan D och F ligger på position 7. Men i position 7 är E:s bit 0, så noden E kommer att vara det vänstra barnet till noden F. Strukturen illustreras nu i figur 13.

Och till sist infogar vi tecken G. Efter alla beräkningar drar vi slutsatsen att den nya noden ska placeras som högra barn till nod F med diff lika med 8. Slutresultatet visas i figur 14.

Hostills har vi infogat strängar som består av endast ett tecken. Vad skulle hända om vi försökte infoga strängarna AB och BA? Den intresserade läsaren kan ta detta förslag som en övning. Två tips: båda strängarna skiljer sig från noden B i position 9, och den slutliga trian illustreras i figur 15.

Om man tänker över den sista figuren kan man ställa sig följande fråga: För att hitta till exempel strängen BA behöver man 5 bitjämförelser, medan det för att beräkna hashkoden för denna sträng endast behövs två iterationer, så när blir PATRICIA Trie konkurrenskraftig? Tänk om vi i denna struktur infogar strängen ABBABABABBBBABABABBA (hämtad från exemplet i PATRICIA:s ursprungliga artikel från 1968) som är 16 tecken lång? Denna sträng skulle placeras som det vänstra barnet till nod AB med diff på position 17. För att hitta den skulle vi behöva 5 bitjämförelser, medan det skulle krävas 16 iterationer för att beräkna hashkoden, en för varje tecken, vilket är anledningen till att PATRICIA Trie är så konkurrenskraftig vid sökning av långa strängar.
PATRICIA Trie vs Hash Map
I det här sista avsnittet kommer jag att jämföra Hash Map och PATRICIA Trie i två tillämpningar. Den första är en ordräkning på leipzig1m.txt som innehåller 1 miljon slumpmässiga meningar och den andra är att fylla en symboltabell med mer än 2,3 miljoner webbadresser från DMOZ-projektet (stängt 2017) som laddas ner härifrån.
Koden som jag utvecklade och använde för att både implementera pseudokoden ovan och för att jämföra PATRICIA Trie-prestanda med Hash Table kan hittas på min GitHub.
De här jämförelserna kördes i min Ubuntu 18.04-box. Konfigurationen finns i figur 16
.