Comparing PATRICIA Trie, With It's Nuts and Bolts, with Hash Map

私が関わっている小宇宙では、トライデータ構造のようなものはそれほど人気があるわけではありません。この環境は主にデータサイエンティストと、少数ですが自然言語処理 (NLP) を扱うソフトウェアエンジニアで構成されています。

最近、trie またはハッシュテーブルをいつ使用するかについての興味深い議論に参加することになりました。その議論では、これら 2 つのデータ構造のそれぞれの長所と短所など、ここで報告できるような新しいことは何もありませんでしたが (少しググれば、それらに言及した多くのリンクが見つかります)、私にとって新鮮だったのは、パトリシアトライと呼ばれる特殊なトライの種類と、いくつかのシナリオにおいて、このデータ構造が処理時間と空間の両方でハッシュテーブルと同等の性能を示し、共通のプレフィックス付きのストリングを追加費用なしにリストするタスクも扱っているということでした。

このことを念頭に置いて、PATRICIA アルゴリズムがどのように動作するのか、特に 1968 年に発表された 21 ページの長い論文を読むための近道として、簡単な方法（怠惰の婉曲表現）で理解できるストーリーやブログはないかと探したのです。

この物語での私の目的は、上記のギャップを埋めること、つまり、手元にあるアルゴリズムを平易な言葉で説明する物語を持つことです。この紹介に続いて、最も一般的なトライをリストアップし、PATRICIAトライがどのように動作し、なぜうまく動作するのかを実装して詳細に説明します。一つは、かなり大きなテキストに基づく単語数（<WORD, FREQUENCY>タプル）、もう一つは、DNSサーバーのコア要素である200万以上のURLのリストに基づいて<URL, IP>タプルを構築するものです。プリンストン大学の Sedgewick と Wayne が Algorithms – Fourth Edition (publisher: Addison-Wesley) で定義したように、トライ（接頭辞木）は「検索を導くために検索キーの文字から構築されるデータ構造」です。この「データ構造は、NULLか他のノードを参照するリンクを含むノードで構成される。各ノードは、その親と呼ばれる他の1つのノードによって指され（ルートという1つのノードを除いて、そのノードを指さない）、各ノードはS個のリンクを持ち、Sはアルファベットサイズ（または文字セット）である」。

上記の定義に従って、下の図1はトライの例を含む。

ルートノードには、ラベルがない。これには3つの子ノードがあり、キー’a’、’h’、’s’を持つノードである。図の右下には、すべてのキーとそれぞれの値をリストアップした表がある。ルートから’a’ -> ‘i’ -> ‘r’へとたどることができる。この順序は、値（例えば、この単語がテキストに現れる回数）が4の単語「air」を形成する（値は緑色のボックスの中にある）。慣習として、シンボルテーブルの既存の単語はヌルでない値を持つ。したがって、”airway” という単語は英語には存在するが、このトライには存在しない。なぜなら、慣習に従って、キー ‘y’ を持つノードの値は null であるからだ。 “airplane “や “airways “などの単語の接頭辞でもあります。 h’ -> ‘o’が “house “と “horse “の接頭辞を形成するように、’h’ -> ‘a’ という並びは “has “と “hat “を形成する。

それは例えば辞書用のデータ構造としてうまく機能するだけではなく、補完アプリケーションの重要な要素として機能する。たとえば、”air” という単語を入力した後に、キー “r” を持つノードをルートとするサブツリーを走査して、”airplane” と “airways” という単語をシステムが提案することができる。この構造のもう1つの利点は、トライを順方向でトラバースし、ノードの子を重ねて左から右にトラバースすることで、追加コストなしに既存のキーの順序付きリストを得ることができることである。

図2にノードの解剖学を例示する。

この解剖学の興味深い点は、子のポインタが通常配列に格納される点である。例えばExtended ASCIIの文字セットSを表現する場合、256のサイズの配列が必要です。子文字があれば、その親のポインタにO(1)時間でアクセスすることができます。語彙の大きさがNで，最長の単語の大きさがMであることを考えると，トライの深さもMであり，構造を走査するのにO(MN)かかることになる．通常NはMよりずっと大きい（コーパスの単語数は最長単語のサイズよりずっと大きい）ことを考慮すると、O(MN)は線形であると考えることができる。さらに単語の平均サイズも M より小さいので、実際には平均して、キーを検索するのに O(logₛ N)、構造全体をトラバースするのに O(N logₛ N)を要する。 1つは空間消費である。 0から始まる各レベルLには、同値でSᴸのポインタが存在する。 Extended ASCII、すなわち256文字では、これは限られたメモリ・デバイスにおける問題ですが、すべてのUnicode文字（そのうちの65,000文字）を考慮すると、状況は悪化してしまいます。 2つ目は、子ノードが1つしかないノードの多さで、入力と検索のパフォーマンスが低下することです。図1の例では、ルート、レベル1のキー「h」、レベル2のキー「a」と「o」、レベル3のキー「r」だけが複数の子ノードを持つ。つまり、27個のノードのうち、2個以上の子ノードを持つのは5個だけである。

代替案（PATRICIA Trie）を説明する前に、次の質問に答えます。配列の代わりにハッシュテーブルが使えるのに、なぜ代替案なのか？ハッシュテーブルは、性能の低下をほとんど伴わずにメモリを節約するのに非常に役立ちますが、問題を解決するものではありません。トライの上位（レベルゼロに近い）ほど、どの文字セットでもほぼすべての文字に対処する必要がある可能性が高くなります。よく実装されたハッシュテーブルは、Javaのもの（間違いなく最高のものの一つで、間違いなく最高です）のように、デフォルトのサイズから始まり、閾値に従って自動的にサイズ変更されます。 Javaでは、デフォルトのサイズは16で、閾値は0.75で、これらの操作のたびにそのサイズを2倍にします。 Extended ASCIIを考えると、1つのノードの子ノード数が192になる頃には、ハッシュテーブルは512にリサイズされ、最終的には256しか必要ないにもかかわらず、です。

Radix Trie

PATRICIAトライはRadix Trieの特殊例ですので、後者を取り上げたいと思います。 Wikipediaでは、基数トライは「空間を最適化したトライを表すデータ構造で、唯一の子である各ノードがその親にマージされる…通常の木（キー全体をその先頭から不等間隔の点まで一括比較する）と異なり、各ノードのキーはチャンクのビットごとに比較され、そのノードにおけるチャンクのビットの量が基数トライの基数rとなる」、と定義されています。この定義は、図3でこのトライを例証すると、より理解しやすくなる。

基数トライのノードの子の数rは、xが上記のチャンクオブビットの比較に必要なビットの数である次の式で決定される：

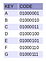
上記の式によって基数トライにおける子の数は常に2の倍数となるよう設定されている。例えば、4Radix Trieの場合、x=2である。これは、2 つのビットのチャンク、ビットのペアを比較する必要があることを意味します。これらの 2 つのビットで 0 から 3 までのすべての 10 進数を表し、合計 4 つの異なる数、各子供に 1 つを表すからです。この例では、5つの文字（NULL、A、B、C、D）からなる仮想的な文字集合があります。 4ビットで表現することにしました（これはrとは関係なく、5文字を表現するのに3ビットで済みますが、例を描きやすくするためです）。図の左上には各文字をビット表現に対応させた表があります。

文字 ‘A’ を挿入するために、NULLの文字とビット単位で比較することにします。図3の右上、黄色い菱形に1と書かれたボックスの中で、この2つの文字が最初のペアで異なっていることがわかる。この最初のペアは、Aの4ビット表現では赤で表されています。つまり、DIFFには、異なるペアが終了するビット位置が含まれています。

文字Bを挿入するには、文字Aとビット単位で比較する必要があります。この比較は2というラベルのついた菱形のボックスで行われます。今回、差は赤で示した2番目のビットの組で発生し、それは位置4で終了します。 2番目のペアは01なので、キーBを持つノードを作成し、ノードAのアドレス01をそれに向けます。このリンクは、図3の下側に見ることができます。

上の例で、最初のペア（青で01）が挿入されるすべての文字のプレフィックスであることが分かる。

この例は、上記の Radix Trie の定義で述べた chunk-of-bits 比較、空間最適化 (文字セットのサイズに関係なく、この場合は 4 つの子のみ)、親子結合 (ルートと異なるビットのみ子ノードに格納) を説明する役割を果たします。それでも、NULLノードを指すリンクが1つ存在する。 Sparsenessはrとtrieの深さに正比例する。

PATRICIA Trie

PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) …。そう、PATRICIAは頭字語なんです!

PATRICIA Trieは、ここでは3つのルールで定義されています。

各ノード（TWINはPATRICIAの原語）は2つの子（Radix Trieの用語ではr = 2とx = 1）を持つ；
ノードは2つの単語（PROPER OCCURRENCEはPATRICIAの用語）が同じプレフィックス（PATRICIAの用語のL-PRHASE）と二つの子（それぞれの子はBRANCHとなり、PATRICIAの元の用語を表す）だけに分裂される；
ノードは1つのプレフィックスと二つの子（PATRICIAの用語のP-PRHAIN)だけが分裂させられる。そして
すべての単語の終わりは、ノード内でnull（PATRICIAのオリジナルの命名法ではENDマーク）以外の値で表される

上記のルール2には、各レベルの接頭辞の長さが前のレベルの接頭辞の長さより大きいことが含まれています。これは、要素の挿入や別の要素の検索といったPATRICIA操作をサポートするアルゴリズムで非常に重要になる。

上記のルールから、以下の図のようにノードを定義することができる。各ノードはルートを除く1つの親と、2つの子、値（任意の型）と、キービットコードにおける分割位置を示す変数diffを持つ

PATRICIAアルゴリズムを使うには、2つの文字列を与えて、左から右へ、両者の異なる最初のビットの位置を返す関数が必要です。これはすでにRadix Trieで動作しているのを見た。

PATRICIAを使ってトライを操作する、つまりキーを挿入したり見つけたりするには、2つのポインタが必要である。一つはparentで、ルートノードを指すことで初期化される。

以下では、挿入されるキーがchild.keyと異なる位置をdiffという変数で保持する。ルール2に従い、以下の2つの不等式を定義する。

不等式 (1)

式（2）

foundはキー検索が終了したノードを指すとする。 found.keyが挿入される文字列と異なる場合、ComputeDiff関数により、この文字列とfound.keyを使用してdiffが計算されます。これらが等しい場合、キーは構造体に存在し、他のシンボルテーブルと同様に、その値が返されます。 BitAtPosition というヘルパーメソッドは、特定の位置 (0 または 1) のビットを取得するもので、操作中に使用されます。

検索するには Search(key) 関数を定義する必要があります。その疑似コードを図4に示す。